Photon Bose-Einstein condensation – Open Quantum Systems

Key publications

J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, ”Bose-Einstein condensation of photons in an optical microcavity”, Nature 468, 545 (2010). link
J. Klaers, F. Vewinger, and M. Weitz, “Thermalization of a two-dimensional photonic gas in a ‘white wall’ photon box”, Nature Physics 6, 512 (2010). link
D. Dung, C. Kurtscheid, T. Damm, J. Schmitt, F. Vewinger, M. Weitz, and J. Klaers, “Variable potentials for thermalized light and coupled condensates”, Nature Photonics 11, 565 (2017). link

Its bosonic and ideal (interaction-free) nature should make a photon gas an obvious candidate for a Bose-Einstein condensation. However, the thermodynamic behavior of photon gases usually does not include a condensation process. For blackbody radiation, the most omnipresent Bose gas, the number of photons follows the available thermal energy. At low temperatures, the photon number simply decreases and no macroscopic occupation of the cavity ground state occurs.

In contrast to a three-dimensional thermal photon gas as Planck’s blackbody radiation, photons can exhibit Bose-Einstein condensation, if the thermalization process is restricted to two motional degrees of freedom. Experimentally, this situation has been realized in a microcavity enclosing a dye medium, designated as a room temperature heat bath for the photon gas. The phenomenon of thermalized light and photonic Bose-Einstein condensates occurs when light inside the microcavity is reabsorbed in the optical medium, thanks to the high reflectivity of the mirrors, instead of being lost through transmission. This reabsorption induces a thermalization process where the photon gas reaches thermal equilibrium with the environment at room temperature. The energies of such thermalized photon gases follow Bose-Einstein statistics, which, at sufficiently high phase space densities, can result in the Bose-Einstein condensation of photons.

Photon condensates have been demonstrated to possess unique first- and second-order coherence properties. The distinctive feature arises from the fact that, unlike atomic condensates, the thermalization process in photon condensates does not occur through interparticle collisions but rather by exchanging energy with a reservoir of electronic excitations stored in the optical medium. In this system, photons can be converted into electronic excitations (and vice versa) through coupling with optically active dye molecules. The best theoretical description for this situation is provided by the grand canonical ensemble statistics, which predicts extremely large statistical fluctuations in the condensate population. For large reservoirs, the statistical fluctuations become as significant as the average particle number, leading to a normalized second-order coherence function approaching g⁽²⁾(0)=2, similar to that of a thermal source. At T=0, this effect is known as the grand canonical fluctuation catastrophe. However, for a small reservoir, the fluctuations remain at a Poisson level with g⁽²⁾(0)=1, resembling the case of Bose-Einstein condensation in the canonical ensemble and also the phenomenon of lasing. Experimentally, the effective size of the reservoir can be adjusted by the dye concentration or the detuning between the zero-phonon line of the dye and the cavity resonance.

In recent years, we haves developed a highly advanced toolbox of experimental techniques around optical microcavities. This applies, for example, to methods of controlling the transverse motion of light in microcavities using nanostructured mirrors and thermo-responsive optical media.

Featured publication

M. Vretenar, C. Toebes and J. Klaers, “Modified Bose-Einstein condensation in an optical quantum gas”, Nature Communications 12, 5749 (2021). link

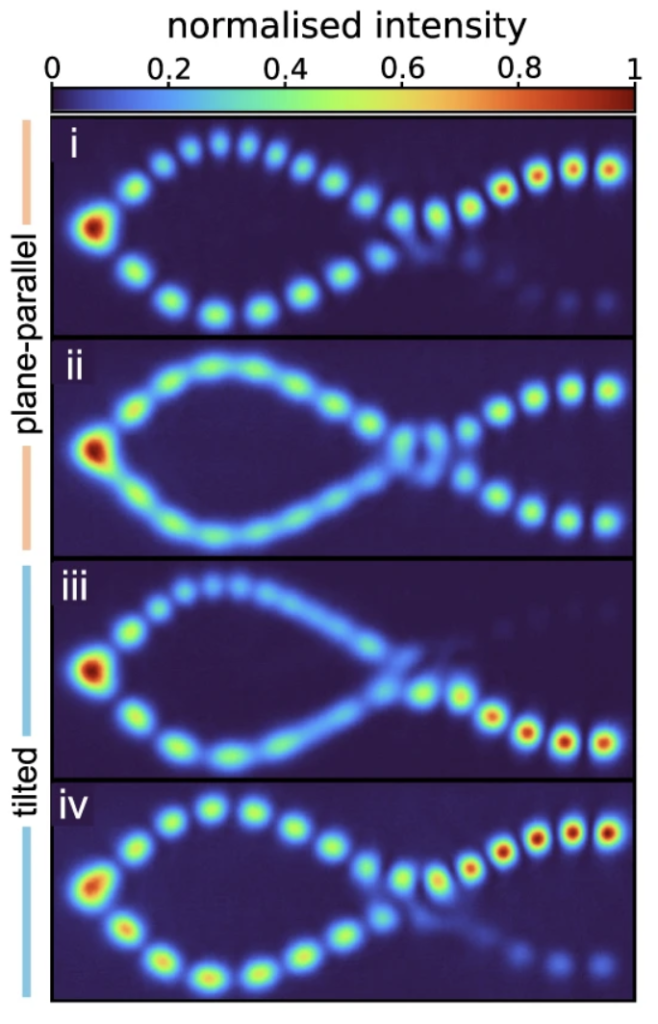
Non-equilibrium and externally controlled quantum systems are currently one of the most active research areas in physics. A main motivation is the fact that such systems are used in emerging quantum technologies such as quantum computing or quantum simulation. An equally important reason is that such systems help us gain a deeper understanding of quantum mechanics. It is often the case that the true character of a physical system only becomes apparent when it is forced to leave its “comfort zone”. One such example is superfluidity. It is only when a superfluid is accelerated from rest that its defining property, i.e., movement without dissipation becomes apparent. Another example concerns the spontaneous emission of an electronically excited atom or molecule. Only when such emitters see an environment other than the usual three-dimensional vacuum do the full mechanisms behind the spontaneous emission reveal themselves. The latter concerns, for example, the role of coherent feedback from the environment.

We also consider the Bose-Einstein condensation to be an example that fits into this list. For the case of thermal equilibrium, it is known that condensation in a Bose gas occurs in the state that minimizes the energy. This is a direct consequence of the Bose-Einstein distribution. But does that really mean that energy is the only criterion in the formation of a Bose-Einstein condensate? In our work, we investigate the Bose-Einstein condensation of a two-dimensional photon gas in an environment with controlled dissipation and feedback realized by a potential landscape that effectively acts as a Mach-Zehnder interferometer. Our measurements offer a highly systematic picture of Bose-Einstein condensation under non-equilibrium conditions. We show that by adjusting their frequency, Bose-Einstein condensates naturally seek to minimize particle loss and destructive interference in their environment. This hitherto unknown ability remains hidden in thermal equilibrium but becomes visible when the condensate is forced to exchange particles with its environment under non-equilibrium conditions. Beyond a deeper understanding of Bose-Einstein condensation, our findings open new pathways for quantum simulations with optical Bose-Einstein condensates.