New publication
V. Sharoglazova, M. Puplauskis, C. Mattschas, C. Toebes, and J. Klaers, “Energy-speed relationship of quantum particles challenges Bohmian mechanics”, Nature 643, 67 (2025). link
Nature News and Views
Nature News
Behind the Paper
Quantum mechanics is compatible with a range of fundamentally different models (often referred to as interpretations), each offering a distinct account of what constitutes physical reality. For example, while the theory is commonly associated with intrinsic randomness, indeterminism is not an established empirical fact. Deterministic models of quantum phenomena exist—most prominently Bohmian mechanics, which posits definite particle trajectories guided by the quantum wave function via the so-called guiding equation. It is often argued that Bohmian mechanics is empirically equivalent to standard quantum mechanics. This equivalence is typically understood in terms of the particle density: if the initial conditions—i.e., the starting points of the Bohmian trajectories—follow the Born rule, then the predicted particle density, averaged over many trajectories, matches that of standard quantum theory. It is further argued that, since every observable can, in principle, be reduced to a position measurement—for example, spin can be inferred from particle trajectories in a Stern–Gerlach experiment—Bohmian mechanics is expected to reproduce all standard quantum measurement predictions.
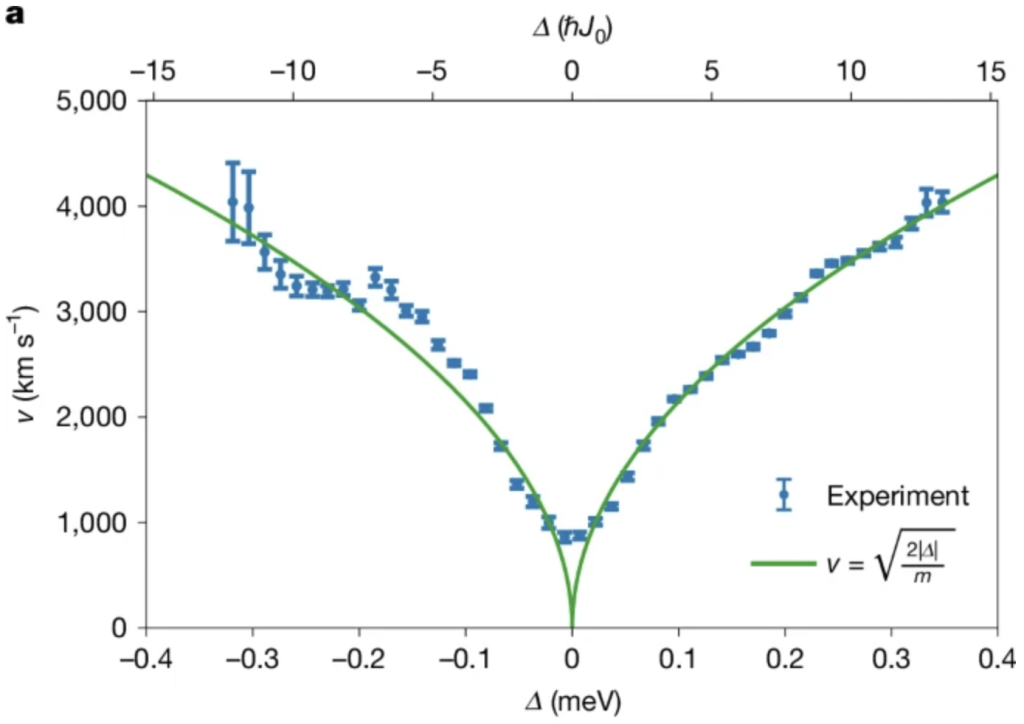
We have recently investigated the particle motion associated with evanescent wave functions, which appear when particles are reflected at a potential step. To do this, we confine the particles to one-dimensional waveguides and couple two such waveguides in a controlled manner by placing them parallel to each other at a close distance. The coupling between the waveguides provides a temporal reference for the particles’ motion. By comparing the motion of particles within a waveguide to the tunneling-induced hopping between the waveguides, we can draw conclusions about how fast the particles move.
The outcome of our experiments is that particles move where they are not expected to move. Contrary to the predictions of the Bohmian guiding equation, which for evanescent wavefunctions suggest that particles are at rest, our experimental results indicate that particles move with a well-defined speed. The measured speed supports the core idea behind de Broglie’s relation: that motion and wavelength are fundamentally linked—albeit with a twist. For evanescent wave functions, we find that a de Broglie relation of the form λ=ℏ/mv holds, where λ is the decay length and v represents the non-directional particle speed that we measure in our experiment. Thus, our results suggest that phase gradients and amplitude gradients play complementary roles in indicating motion within a quantum mechanical wave function. This stands in contrast to the guiding equation in Bohmian mechanics, which attributes motion solely to phase gradients. In other words, our findings call into question whether the ontology implied by Bohmian trajectories is realized in nature.