New publication
J. Klaers, V. Sharoglazova and C. Toebes, “Particle motion associated with wave-function density gradients”, Physical Review A 107, 052201 (2023). link
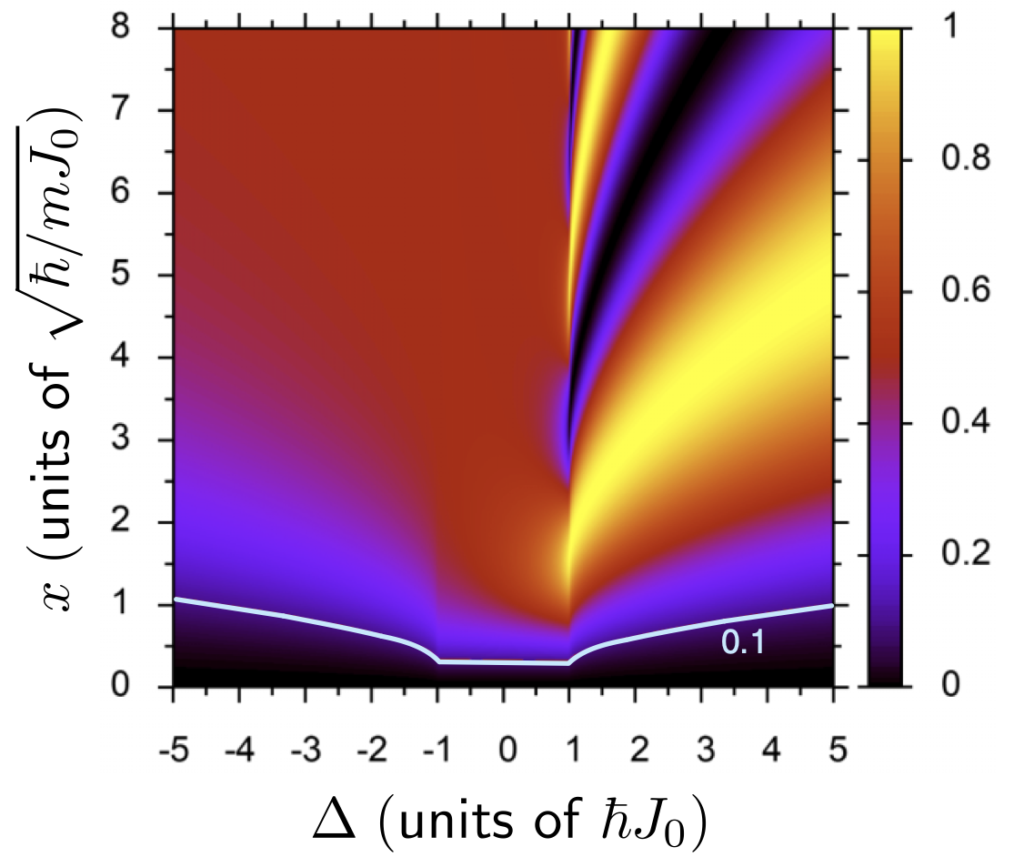
In our everyday life, it seems obvious that physical objects have a position and a velocity. This intuitive understanding is, however, seriously challenged by quantum mechanics. Quantum mechanics knows a variety of velocity definitions such as group velocity, phase velocity, velocities derived from the momentum operator or from the probability flow. However, their physical meaning is not always obvious and may not correspond to our classical understanding of motion.
Assigning a velocity to a wavefunction is possible in some cases, such as with Gaussian wave packets, and may even fit our classical intuition of motion quite well. However, the situation becomes much less obvious when this wave packet meets a reflective potential step, so that the oscillating behavior of the wavefunction turns into an exponential decay. Is it still possible to assign a physically meaningful velocity to the exponentially decaying part of the wavefunction? This question was the starting point for our work.
To investigate this question, we have adapted an approach known from tunneling time research, the so-called Larmor clock, for our purposes. This approach basically means adding additional degrees of freedom to the system, the change of which can be understood as a measurement of time. More specifically, we study the quantum mechanical motion of massive particles in a system of two coupled waveguide potentials, where the population transfer between the waveguides effectively acts as a clock and allows particle velocities to be determined. The application of this scheme to tunneling phenomena at a reflective step potential leads to the main results of our work, namely an energy-velocity relationship for classically forbidden motion.